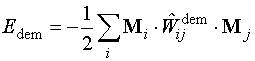Theoretical background

I. Basic micromagnetic concept and main energy contributions

Theoretical micromagnetics as founded by W.F.Brown is a phenomenology for the evaluation of the total magnetic free energy Etot of a ferromagnetic body if its geometry, material parameters and the magnetization configuration are known. In its 'minimal' version micromagnetics takes into account four energy contributions:


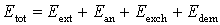
Energy in the external field E_ext:


Magnetocrystalline anisotropy energy E_an (e.g., uniaxial case):


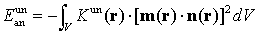
Exchange stiffness energy E_exch (isotropic exchange assumed):


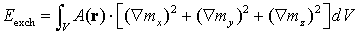
Magnetodipolar interaction energy (stray or demagnetizing) field energy E_dem:


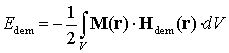
where the demagnetizing field H_dem can be calculated as a convolution of the magnetization distribution inside a ferromagnet with the dipolar interaction kernel.

II. Finite-difference approximations of the energy contributions used in MicroMagus

Notation:

M_i - magnetization in the cell # i, m_i = M_i/M_i
H_i^ext - external field averaged over the cell # i
DV_i - cell volume

1. External field


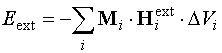
2. Anisotropy (K_i – anisotropy constants)

• uniaxial (n_i – unit vector of the anis. axis)

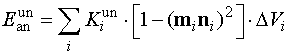
• cubic (p_x,y,z – components of the unit magn. vector in a local coord. system)

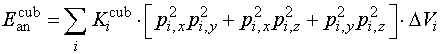
3. Exchange (J_ij – exchange coeff., k_ij – exch. weakening, a_ij – angle between M_i and M_j)


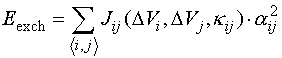
4. Stray field (W_ij – interaction coeff. between cells i and j)